揭秘有限元中的“KUG”：它究竟代表什么？

无尽之路安多克洛斯迷宫官方版(迷宫冒险类手游) v1.3 安卓版 67.27M / 简体中文

点击下载

黑暗托儿所安卓版(暗黑解谜手游) v1.4 手机版 92.66M / 简体中文

点击下载

染上绯色中文版(文字冒险游戏) v1.9 安卓汉化版 59.85M / 简体中文

点击下载

在探讨工程技术和数学应用的广阔领域中，有一个概念频繁出现却常被非专业人士所忽视，那就是“有限元”中的KUG。听起来或许有些晦涩难懂，但请跟随我们的步伐，一起揭开KUG在有限元分析中的神秘面纱，看看这个看似复杂的术语如何在工程实践中发挥至关重要的作用。

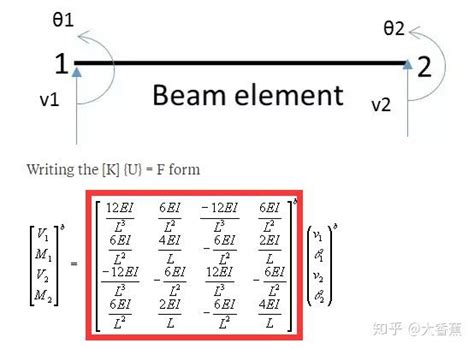
有限元法（Finite Element Method，简称FEM）是数学中的一种数值技术，它用于求解偏微分方程的边值问题。简单来说，有限元法是一种将复杂问题简化为更小、更易管理的部分（即“有限元”）的方法。这些有限元通过节点相互连接，形成一个整体，从而允许我们通过计算每个单元的行为来推断整个结构的行为。这一方法的核心思想，就如同用多段微小的直线来逼近一个圆的形状，它通过将大的、复杂的问题分解成小的、简单的部分，使得计算变得可行且准确。

有限元法起源于航空力学，其基本概念最早在1943年由Courant提出，但直到1960年，随着美国学者Clough的工作，有限元这一学科才真正确立起来。中国数学家冯康也独立对有限元法做出了重要贡献。随着电子计算机的发展，有限元法迅速崛起，成为解决复杂工程问题的重要工具。它不仅广泛应用于固体力学、流体力学、热传导、电磁学等领域，而且在生物力学、声学等多物理场耦合分析中展现出巨大的潜力。

在有限元分析中，KUG是一个至关重要的概念。KUG，全称为“三维单元的刚度矩阵”（Stiffness Matrix in Three Dimensions），是描述三维结构体单元在受载时刚度响应的矩阵。这个矩阵由节点的自由度组成，它根据材料的弹性模量、泊松比以及单元的几何形状等参数计算得出。KUG矩阵的重要性在于，它将物体的几何特征和材料性能结合起来，为工程师提供了一种强大的工具来分析物体的行为。

想象一下，当你设计一座桥梁或一座建筑时，你需要确保它在各种载荷作用下都能保持稳定和安全。这就需要用到有限元分析，而KUG矩阵正是这一分析的核心。通过计算每个单元的刚度矩阵，你可以了解结构在受到外力作用时的变形情况，进而评估其安全性和稳定性。

KUG矩阵的计算过程涉及多个参数的复杂相互作用。首先，你需要知道材料的弹性模量和泊松比，这些参数描述了材料在受力时的变形特性。其次，你需要了解单元的几何形状和尺寸，因为形状和尺寸的不同会显著影响单元的刚度。最后，通过将这些参数输入到有限元软件中，软件会自动计算每个单元的刚度矩阵，并将它们组合起来形成一个整体的结构刚度矩阵。

在有限元分析中，结构被离散化为许多小的单元，每个单元都有一个与之对应的刚度矩阵。这些刚度矩阵通过节点相互连接，形成一个大型的整体刚度矩阵。当结构受到外力作用时，整体刚度矩阵会发生变化，从而反映结构的变形情况。通过求解这个整体刚度矩阵，我们可以得到结构在受力作用下的位移、应力和应变等关键信息。

有限元法的优点在于其强大的适应性和准确性。它可以处理各种复杂形状和边界条件的问题，而且计算精度很高。这使得有限元法成为工程师和科学家在解决复杂工程问题时的首选工具。此外，有限元法还可以与其他数值方法（如有限差分法、有限体积法等）相结合，形成更加灵活和强大的分析工具。

随着计算机技术的不断发展，有限元分析（Finite Element Analysis，简称FEA）在工程领域中的应用越来越广泛。它不仅用于桥梁、建筑等大型结构的设计和分析，还广泛应用于汽车、飞机、船舶等交通工具的碰撞模拟和性能优化。此外，在生物医学工程中，有限元分析也被用于模拟人体组织的受力情况和手术过程中的生物力学效应。

KUG矩阵在有限元分析中的核心地位不容忽视。它是连接材料性能、几何形状和结构行为的桥梁。通过精确计算每个单元的刚度矩阵，我们可以得到整个结构的精确行为预测。这不仅提高了工程设计的准确性和可靠性，还大大降低了设计和测试的成本和时间。

然而，有限元分析并不是万能的。它依赖于准确的输入参数和合理的模型假设。如果输入参数不准确或模型假设不合理，那么分析结果将失去意义。因此，在进行有限元分析时，我们需要仔细考虑模型的简化程度、参数的取值范围以及边界条件的设置等因素。

此外，有限元分析还需要强大的计算能力支持。虽然随着计算机技术的不断发展，计算能力已经不再是制约有限元分析应用的瓶颈，但对于大型复杂结构来说，计算仍然需要耗费大量的时间和资源。因此，如何优化有限元分析的算法和流程，提高计算效率，仍然是当前研究的热点之一。

尽管存在这些挑战和限制，有限元分析仍然以其强大的功能和广泛的应用领域而备受推崇。KUG矩阵作为有限元分析中的关键概念之一，不仅帮助我们理解了结构在受力作用下的行为特征，还为工程设计和优化提供了有力的支持。

在未来的发展中，有限元分析将继续在各个领域发挥重要作用。随着计算机技术的不断进步和算法的不断优化，有限元分析将更加高效和准确。同时，随着多物理场耦合分析的兴起和复杂工程问题的不断涌现，有限元分析也将面临更多的挑战和机遇。然而，无论未来如何变化，KUG矩阵作为有限元分析中的核心概念之一，都将继续发挥着不可替代的作用。

总之，有限元中的KUG矩阵是一个看似复杂却至关重要的概念。它通过将物体的几何特征和材料性能相结合，为工程师提供了一种强大的工具来分析结构的行为。随着计算机技术的不断发展和有限元分析方法的不断优化，KUG矩阵将在未来的工程设计和优化中发挥越来越重要的作用。希望这篇文章能够帮助你更好地理解KUG在有限元分析中的意义和作用，激发你对这一领域的兴趣和探索精神。